در این مقاله قصد دارم مطالبی بسیار سودمند و مهم در مورد تئوری ارتعاشات ماشین (Vibration Theory)، با شما به اشتراک بگذارم.
- تئوری ارتعاشات ماشین: جرم و فنر و دمپر
- معادله دینامیکی روتور توربین چگونه به دست می آید؟
- مدل کردن نیروی آنبالانسی در روتور توربین به کمک تئوری ارتعاشات ماشین
- کاربرد تئوری ارتعاشات ماشین در عیب یابی از ماشین های دوار
- مقادیر زاویه فاز و دامنه برحسب دور ماشین و نسبت میرایی
- یک سیستم چند فرکانس طبیعی دارد؟
- محاسبه فرکانس های طبیعی سیستم چه اهمیتی دارد؟
تئوری ارتعاشات ماشین جرم و فنر و دمپر
معمولاً در کلاسها و کارگاههای آنالیز ارتعاشات، برخی از دانشجوها هنگام تدریس بخش تئوری ارتعاشات، بهشوخی به من میگویند: ما در محل کارمان، اینهمه دور ماشین گشتیم؛ ولی فنر و دمپر ندیدیم! چرا از دانشگاه تا محل کارمان، این روابط ریاضی بیان میشود؟ در این مقاله به این سوال شما پاسخ داده میشود.
مدل کردن روتور توربین
روتور توربین در معرض انواع مختلف نیرو و گشتاور قرار میگیرند. این نیروها میتوانند استاتیکی (بدون تغییر در جهت و زمان) و یا دینامیکی باشند که میتوانند در اندازه یا جهت با زمان تغییر کنند. نیروهای استاتیکی که بر روی سیستم روتور وارد میشوند باعث تغییر شکل استاتیکی عناصر سیستم روتور میشوند. به عنوان مثال یک بار شعاعی استاتیک اعمال شده به وسط یک روتور توربین به تغییر شکل روتور در جهتی متفاوت از بار اعمال شده منجر میشود. یا هنگامی که یک گشتاور پیچشی به روتور یک توربین در حال کار اعمال می شود، روتور در پاسخ به آن تا حدی میپیچد. نیروهای دینامیکی وارد بر روی سیستم روتور باعث تولید ارتعاش میشوند. ارتعاش میتواند به صورت ارتعاش شعاعی، محوری و پیچشی ظاهر شود. ارتعاش محوری میتواند در حین پدیده سرج در کمپرسورها یا بخاطر مشکلات پیستون بالانس یا مشکلات کوپلینگ در مجموعه ماشینها رخ دهد. ارتعاش پیچشی میتواند به دلیل تغییرات در هندسه ی دندانه تماس متناوب روتور و استاتور، فركانس لغزش موتور الکتریکی یا نامنظم بودن گشتاور پیچشی کوپلینگهای ناهمراستا محرکها یا بارهای رفت و برگشتی یا بخاطر ارتعاش شعاعی رخ دهد.
شایان ذکر است که معمولا با ارتعاش محوری کمتر مواجه میشویم اما میتواند مشکلاتی در توربین ایجاد کند. اندازه گیری ارتعاش پیچشی بسیار دشوار است و معمولاً نادیده گرفته می شود. اگرچه هر دو ارتعاش پیچشی و محوری میتوانند از طریق مکانیزمهای کوپل متقابل موجود در ماشینهای دوار، ارتعاش شعاعی ایجاد کنند اما معمولاً ارتعاش شعاعی را در ماشینهای دوار اندازه گیری میشود زیرا ارتعاش شعاعی رایجترین مشکل ارتعاشی ماشین ها است.
سوال مهم: چطور با اندازه گیری ارتعاشات روتور یک توربین، به ماهیت نیروهای تولید کننده این ارتعاش پی ببریم؟
در پاسخ باید گفت: یک مدل خوب به ما این امکان را میدهد که ارتعاش مشاهده شده را با نیروهایی که بر روی سیستم وارد میشوند مرتبط کنیم. این به ما را امکان میدهد مشکلات احتمالی در سیستم روتور را شناسایی و تصحیح کنیم به عبارت دیگر، یک مدل خوب همچنین به ما این توانایی را میدهد که پیش بینی کنیم چگونه تغییرات نیروها بر ارتعاش تأثیر میگذارد.
فرض کنید میخواهید شفت یک توربین را به سادهترین شکل ممکن، مدل کنید. بنابراین و همانطور که در شکل 3-1 مشاهده میکنید، تمام جرم شفت توربین را در مؤلفهای به نام «m» قرار میدهید.
خاصیت کشسانی آن را با فنری به سختی «k» شناخته میشود را چطور معادل میکنید؟ در پاسخ باید گفت: ارتعاش سیستم روتور با تبدیل انرژی از انرژی جنبشی حرکت به انرژی پتانسیل اعضایی همانند فنر همراه است انرژی پتانسیل میتواند بطور موقت در تغییر شکل شفت روتور، تغییر شکل یاتاقان، تغییر شکل پوسته ماشین، تغییر شکل سیستم لوله کشی متصل و تغییر شکل سیستم فونداسیون ذخیره شود. بصورت مجازی هر عضوی از سیستم روتور میتواند مثل یک فنر عمل کند که برای ذخیره موقت انرژی ارتعاشی در دسترس است. همچنین میرایی سیستم که عامل مقاومت در برابر حرکت است (مثلاً اصطکاک شفت توربین با فیلم روغن یاتاقانهای ژورنال) و باعث میراشدن موج ارتعاشی میشود را در مؤلفهای به نام «c» قرار میدهید.
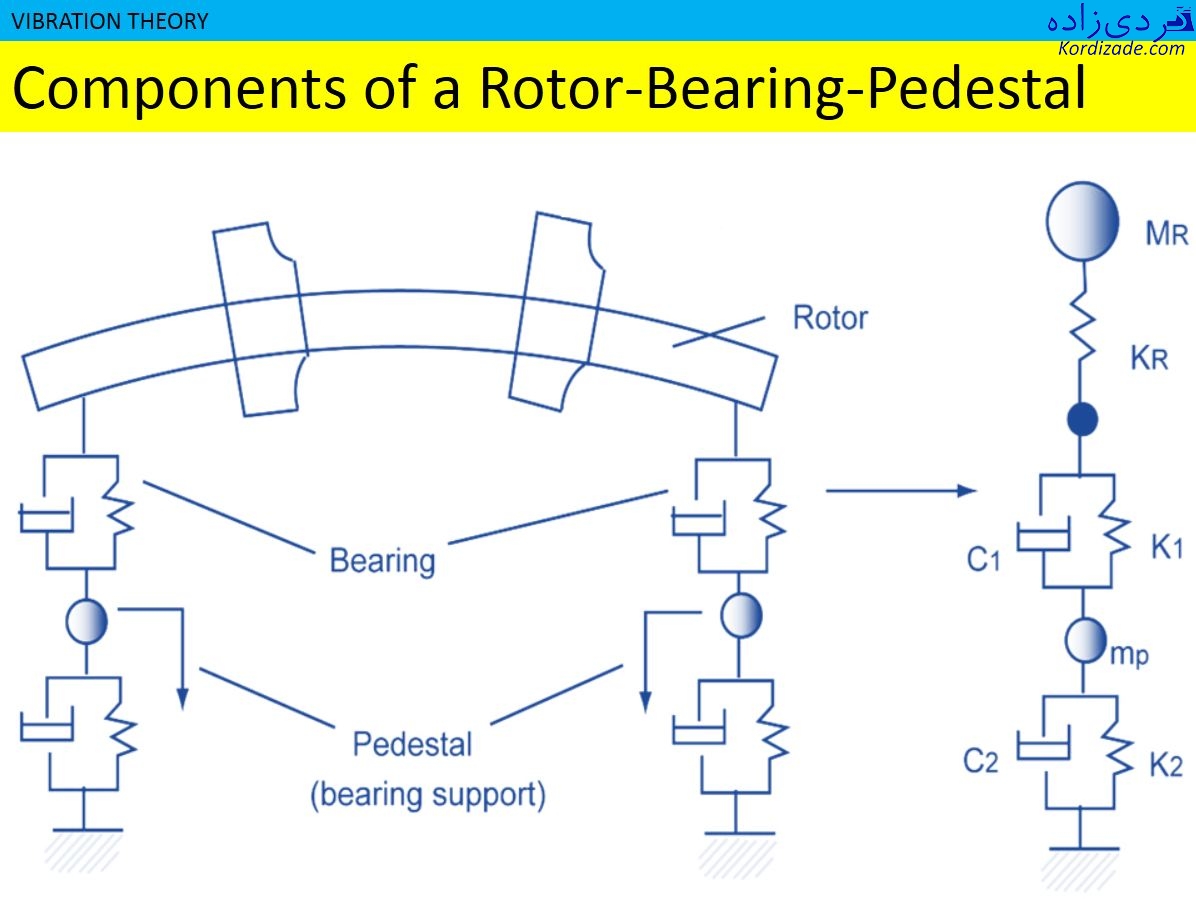
ارتعاش آزاد
سادهترین معادله دینامیکی شفت این توربین را با فرض ارتعاشات خطی و آزاد یک سیستم یک درجه آزادی، به قرار معادله زیر بیان مینمایید: سیستم یک درجه آزادی اهمیت ویژه ای در ارتعاشات دارد. علت آن است که بسیاری از خواص ارتعاشی یک سیستم را میتوان با مدل یک درجه آزادی تشخیص داد. به عنوان مثال، نوسان بال هواپیما را میتوان با یک جرم و فنر و دمپر مدل سازی نمود. ازطرفی میتوانیم یک سیستم با بینهایت درجه آزادی را با بینهایت سیستم یک درجه آزادی مدل نماییم. از این منظر شناخت سیستم یک درجه آزادی اهمیت ویژهای دارد. به عبارت دیگر، سیستم یک درجه آزادی مشابه حروف الفبای یک زبان است. با ترکیب سیستمهای یک درجه آزادی، سیستمهای چند درجه آزادی تولید میشوند که مشابه کلمات یک زبان هستند و زمانی که سیستمهای چند درجه آزادی با یکدیگر ترکیب شوند، سیستم پیوسته تولید میشود که سیستم پیوسته همانند جمله کامل در یک زبان است. پاسخ معادله بالا (یعنی ) پاسخ شفت توربین در حالت ارتعاشات آزاد است و در شکل 3-2 آورده شده است.
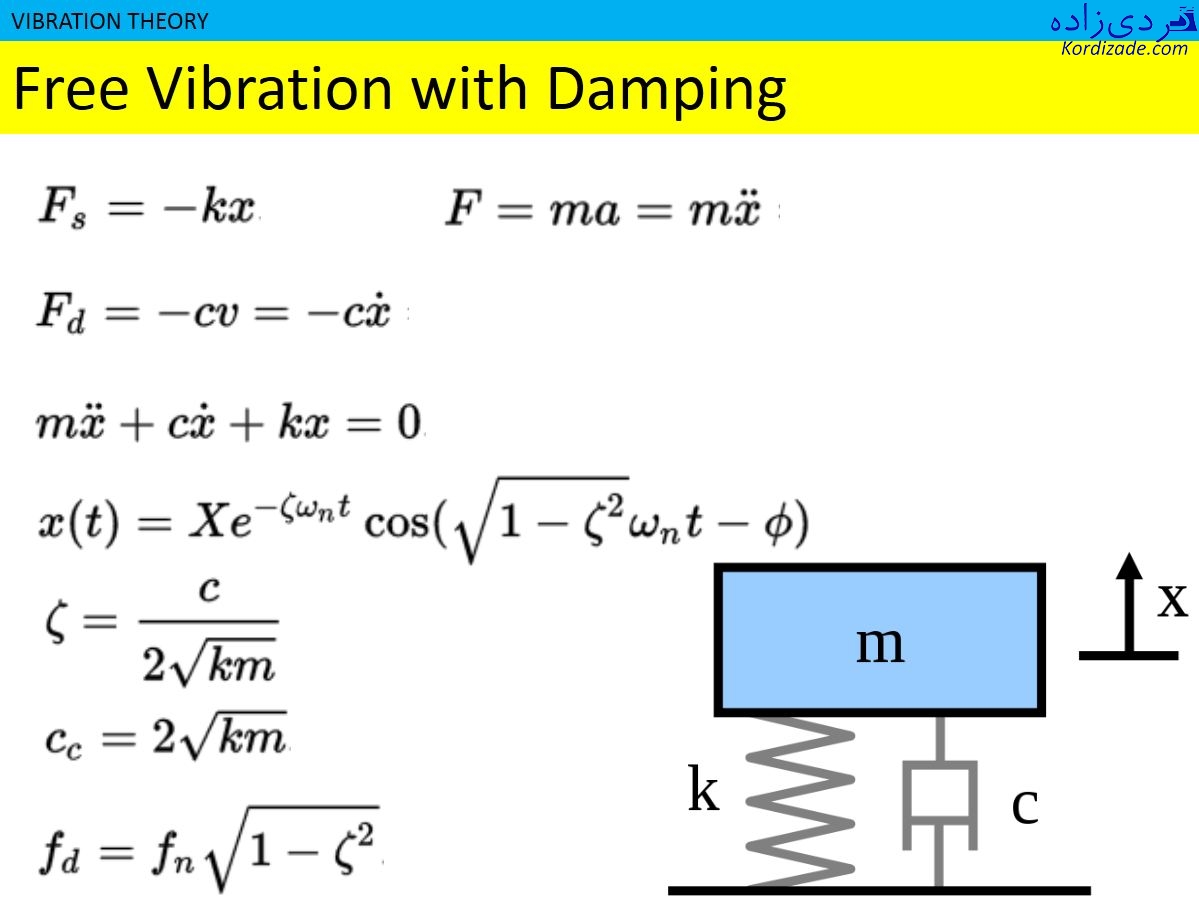
ارتعاش اجباری
در قبل قبلی در خصوص ارتعاش آزاد مطالبی ارئه شد اما در عمل، شفت توربین همواره تحتتأثیر نیروهای تحریک خارجی[Excitation Force] مانند تحریکهای زمانی و تحریکهای هارمونیک قرار دارد. تحریکهای زمانی (ضربه، پالس، رمپ ..) برای ما جذاب هستند. زیرا هر نیروی خارجی را میتوان به کمک سری تیلور به نیروی ضربه، پالس، رمپ و .. تجزیه کرد و لذا به کمک جمع آثار و با داشتن جواب هرکدام از این بخشها و ترکیب آنها به پاسخ سیستم نسبت به یک نیروی خاص دست میابیم.
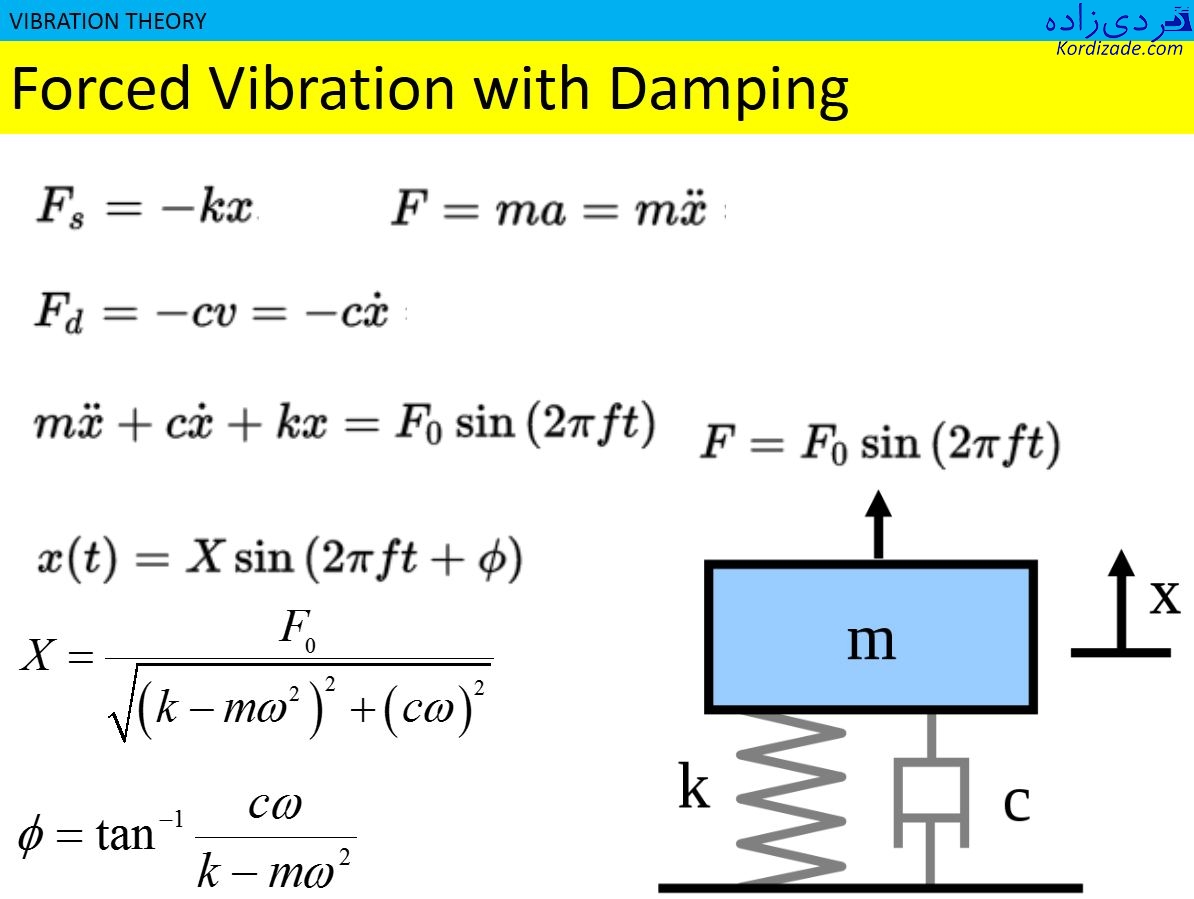
دومین دسته تحریکهای هارمونیک هستند. زیرا میتوان هر تحریک پریودیک دلخواهی را به کمک بسط فوریه برحسب تحریکهای هارمونیک مجزا تفکیک نمود. به عنوان مثال، توابع سینوسی با تولید نیروهای هارمونیک، یکی از شایعترین نوع نیروهای تحریک هستند و با پدیدههای فیزیکی مانند آنبالانسی، بهخوبی تطابق دارند. در این حالت، معادله دینامیکی شفت توربین با فرض ارتعاشات اجباری یک سیستم یک درجه آزادی تحت نیروی تحریک هارمونیک، به صورت زیر بیان میشود:
پاسخ معادله بالا، در شکل زیرنشان داده شده است.
حتما پیشنهد میکنم مقاله “آنبالانسی چیست و چه عواملی باعث ایجاد آنبالانسی میشود؟” را از طریق لینک زیر مطالعه کنید.
“آنبالانسی چیست و چه عواملی باعث ایجاد آنبالانسی میشود؟”
پاسخ معادله دارای دو پاسخ همگن [Homogenous Solution] و پاسخ خصوصی [Particular Solution] است.
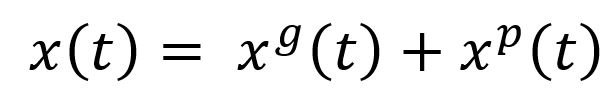
جواب همگن، پاسخ سیستم به ارتعاشات آزاد است و با عبارت زیر بیان میشود:
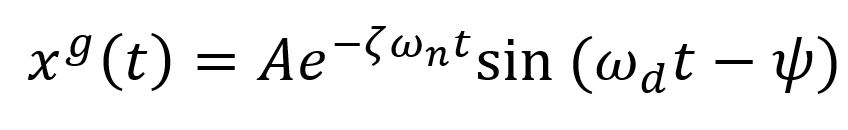
با توجه به ترم 
در پاسخ همگن، این پاسخ با گذشت زمان، به سمت صفر میل میکند. به عبارت دیگر، پاسخ گذرای مسئله است و با گذشت زمان، از بین میرود.
پاسخ خصوصی این معادله، به ارتعاشات اجباری شفت توربین تحتتأثیر نیروی تحریک هارمونیک مربوط است و چون میرا نمیشود، پاسخ پایدار سیستم است و به صورت زیر بیان میشود:
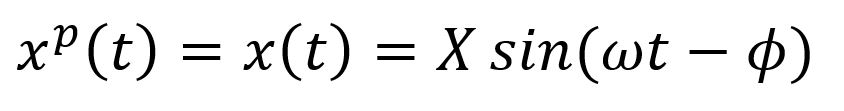
شایان ذکر است، جواب بالا با فرض خطی بودن سیستم است. به عبارت دیگر اگر یک سیستم خطی تحت یک ورودی در یک فرکانس خاص (در اینجا ) قرار گیرد، این فرکانس ورودی در پاسخ خروجی ظاهر میشود.
مقادیر و برحسب فرکانس ، سختی شفت توربین و جرم شفت توربین ، به این صورت محاسبه میشود:
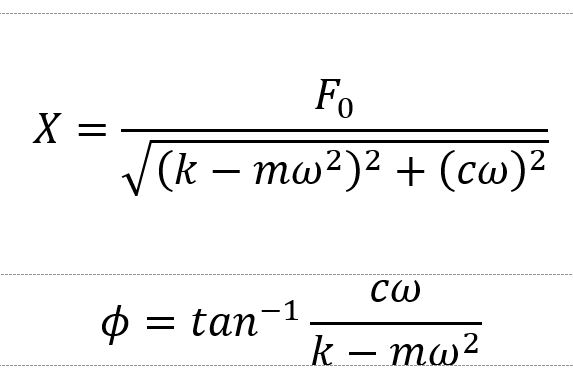
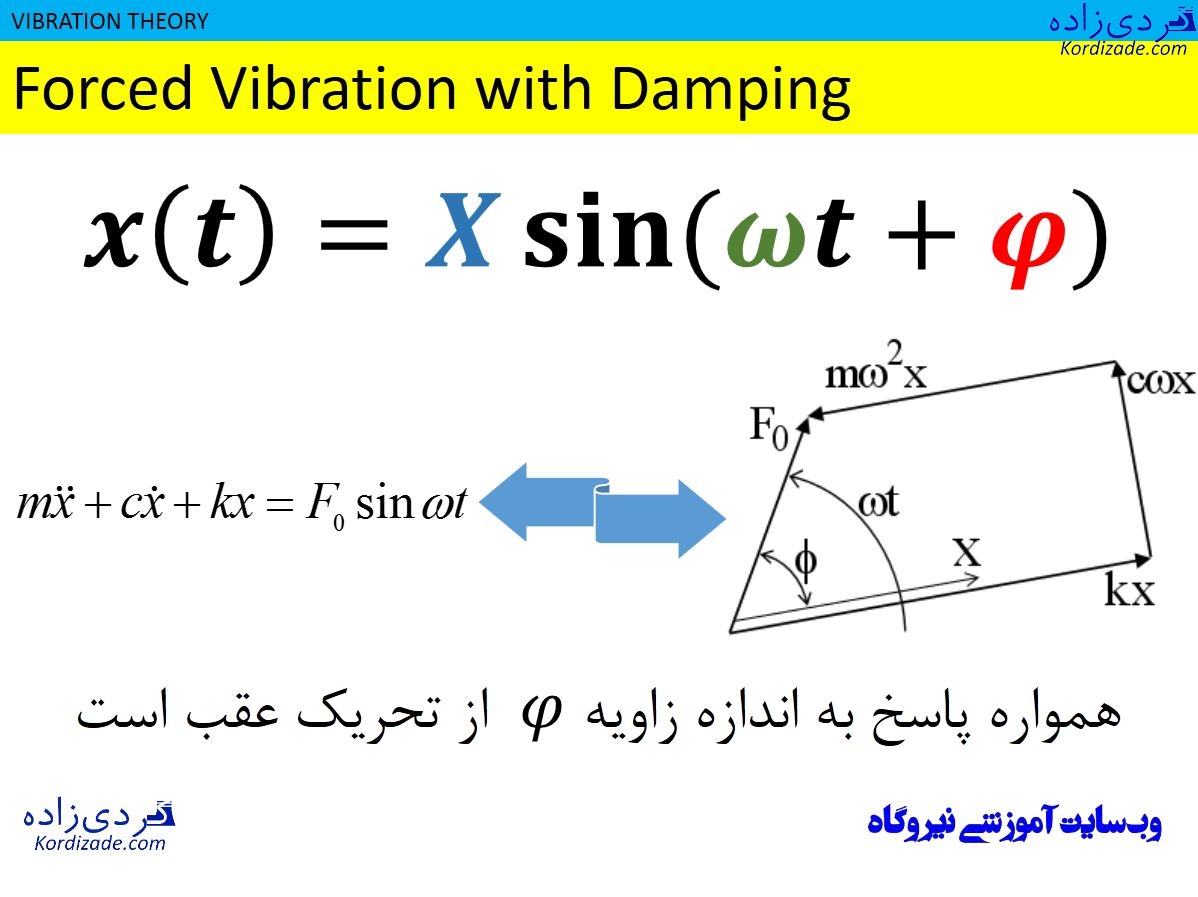
همانگونه که در شکل زیر مشاهده میکنید، معادله نیروی تحریک و پاسخ، فرکانس یکسانی دارند؛ اما پاسخ از نیروی تحریک به اندازه عقب است.
کاربرد تئوری ارتعاشات ماشین در عیب یابی از ماشین های دوار
نکته زیبایی که اینجا وجود دارد این است که، نیروی آنبالانسی و پاسخ، فرکانس یکسانی دارند و این نکته در عیب یابی ماشین بسیار سودمند می باشد. از طرفی، پاسخ از تحریک به اندازه زاویه Φ عقب می باشد.
مقادیر زاویه فاز و دامنه برحسب دور ماشین و نسبت میرایی
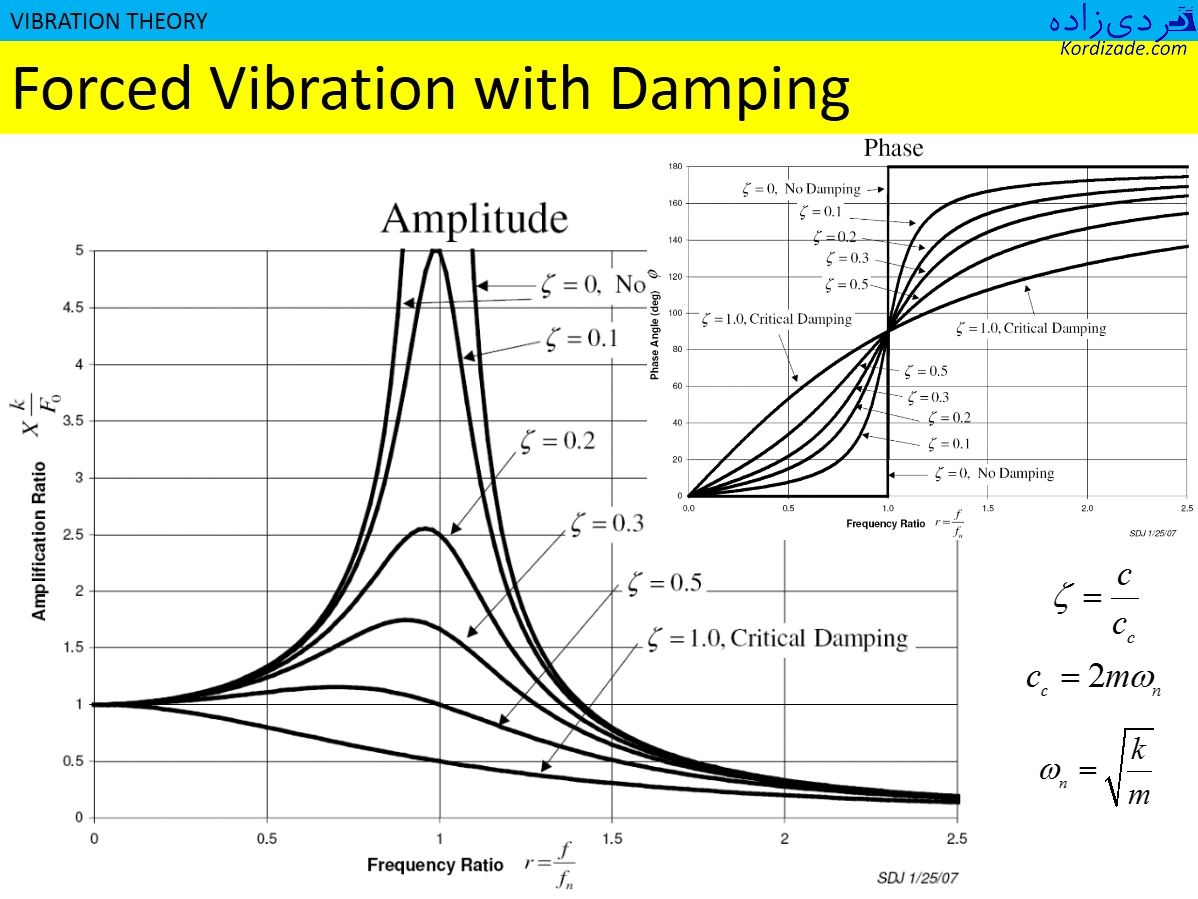
در تئوری ارتعاشات ماشین، نمودارهایی مقادیر زاویه فاز و دامنه برحسب دور ماشین و نسبت میرایی، مدل میکنند. همانطوری که در این نمودارها مشاهده می کنید، وقتی که دور ماشین به فرکانس طبیعی ماشین نزدیک می شود، دامنه روند افزایشی پیدا میکند. این مسئله نشان دهنده اهمیت وجود فیلم روغن را در ماشین هایی بزرگ همانند توربین ها، می باشد. ماشین های بزرگ مانند توربین ها، قادر به عبور از فرکانس طبیعی یا سرعت بحرانی (Critical Speed) به وسیله بلبرینگ (Ball Bearing) نبوده و مجبور هستید از یاتاقان ژورنال استفاده کنید.
نکته دیگری که در این نمودار وجود دارد این است که، بعد از اینکه دور ماشین از فرکانس طبیعی اولش عبور میکند، دامنه ارتعاشات ماشین کاهش میابد. این مسئله نشان دهنده این است که ماشین های بزرگ بعد از عبور از فرکانس طبیعی اول، نرمتر کار میکنند. همانطور که در منحنی زاویه فاز برحسب دور ماشین مشاهده میکنید، در سرعت بحرانی، تمام منحنی ها از عبور میکنند. این نکته خیلی مهم در تشخیص فرکانس طبیعی بسیار سودمند است. به این صورت که فرکانس طبیعی ماشین جایی است که زاویه فاز 90 درجه و مقدار دامنه ارتعاش، ماکزیمم (maximum) می باشد.
با مفهوم زاویه فاز بیشتر آشنا شوید.
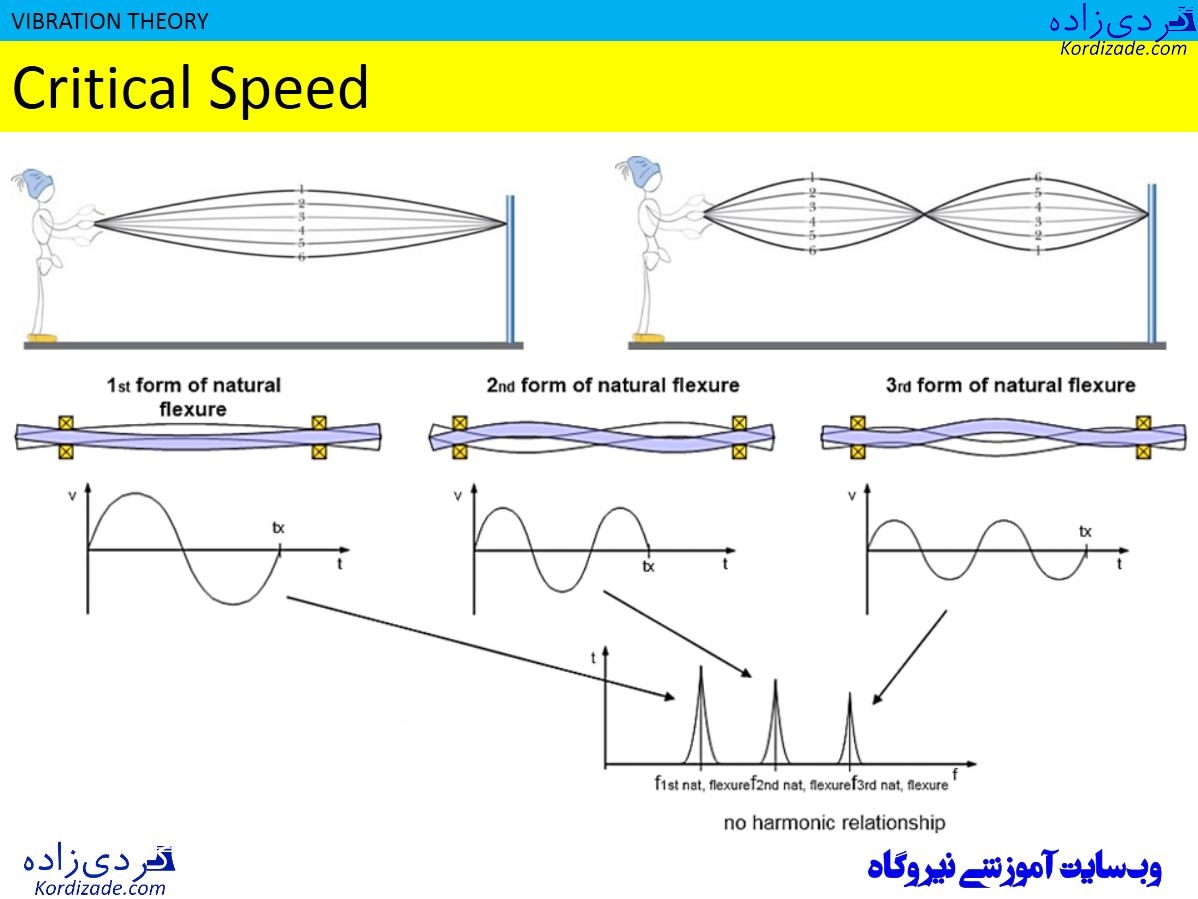
یک سیستم چند فرکانس طبیعی دارد؟
شاید بپرسید که یک ماشین، برای مثال شفت توربین، چند فرکانس طبیعی دارد؟ در پاسخ باید بگوییم که كمترين تعداد مختصات مورد نیاز براي مشخصكردن كامل موقعيت همه قسمتهای يك سيستم را در هر لحظه از زمان، درجه آزادی سیستم[Degrees of Freedom] (DOF) مینامند. برای مثال، حركت پاندول ساده را میتوان تنها با يك مختصات و با زاويه آن حول محور چرخش، نشان داد. بنابراين سيستمی با درجه آزادي ساده است. اما شفت توربین، بینهايت نقاط جرم دارد و در نتیجه، برای مشخصشدن تغییر شکلش، به بینهايت مختصات نیاز دارد. هرچه تعداد درجه آزادي بيشتر شود، سيستم پیچیدهتر میشود. بنابراین ماشین پیچیدهای مانند شفت توربین، بینهايت درجه آزادی و بینهایت فرکانس طبیعی دارد و تعداد فرکانسهای طبیعی آن، به شیوه مدلکردن شفت توربین بستگی دارد. هرچه در مدل ریاضی از عنصرهای جرم، فنر و دمپر بیشتری استفاده شود، به همان میزان، تعداد فرکانسهای طبیعی بیشتری از شفت توربین به دست میآید.
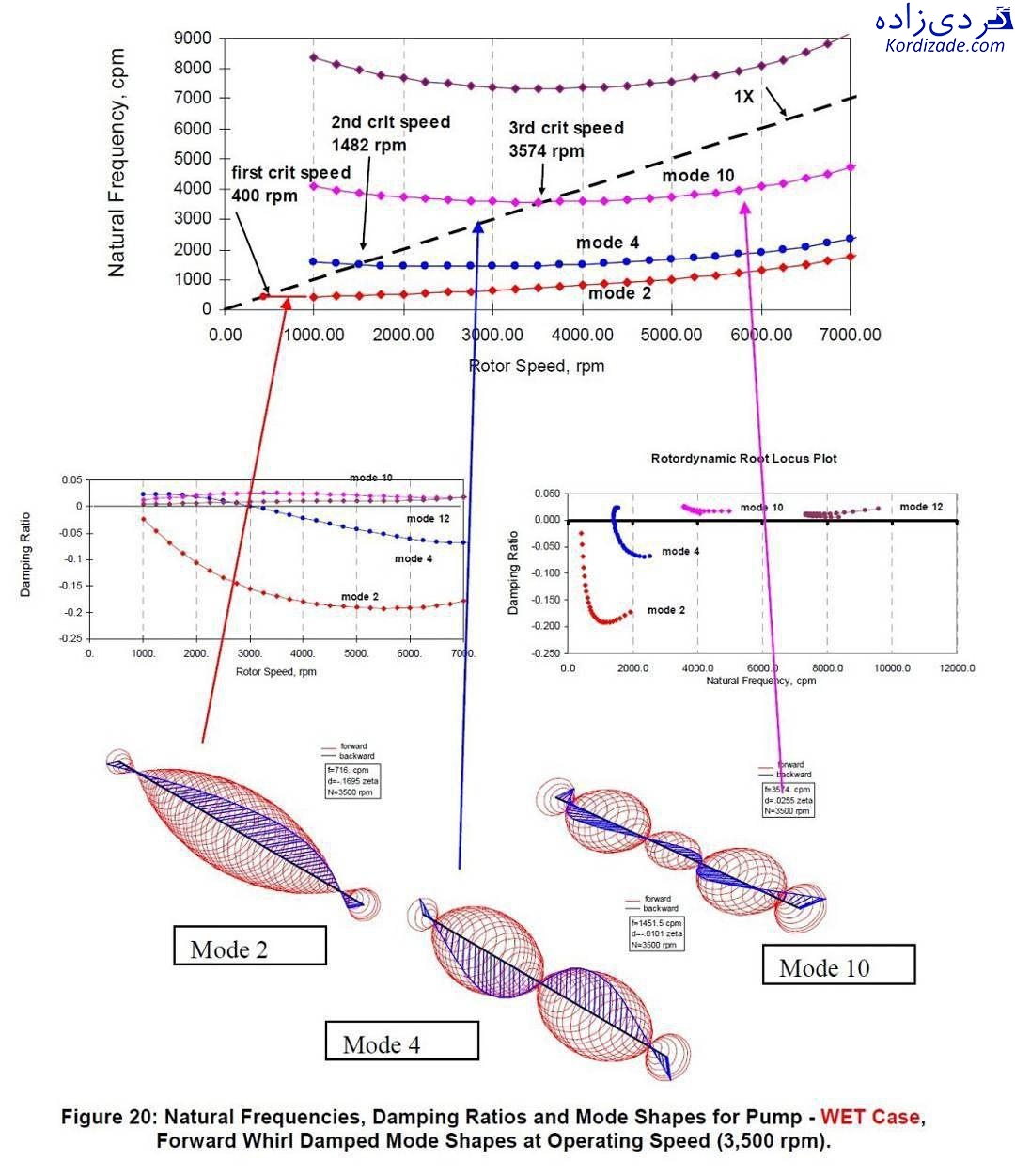
آیا آگاهی از همه فرکانسهای طبیعی ماشین، ضروری است؟
برای جلوگیری از رزونانس، باید به آن دسته از فرکانسهای طبیعی سیستم توجه کنیم که مقادیر آنها، کمتر از فرکانس کاری ماشین است. برای مثال، در الکتروموتورهای کوچک، فاصله تکیهگاههای نگهدارنده روتور از یکدیگر، کم است و به همین دلیل، الکتروموتور کوچک معمولا شفت با سختی بالایی دارد. همچنین الکتروموتور کوچک جرم کمتری دارد.
از آنجایی که فرکانس طبیعی با رابطه 
تعیین میشود، بنابراین رابطه فرکانس طبیعی با مجذور سختی، مستقیم و با جرم، عکس است. از این رو، مقدار فرکانس طبیعی در الکتروموتور کوچک، عدد بزرگی است و معمولاً از فرکانس کاری الکتروموتور، بهمراتب بیشتر است. در نتیجه، محاسبه فرکانس طبیعی برای الکتروموتورهای کوچک، اهمیت چندانی ندارد؛ اما الکتروموتورهای بزرگ برعکس این حالت هستند و برای همین، تا چهار فرکانس طبیعی را در ژنراتورها محاسبه میکنند.
برای دانلود مقاله « تئوری ارتعاشات، دوماهنامه نگهداری و تعمیرات در صنایع نفت، گاز و پتروشیمی، سال ششم، شماره سی و سوم، صفحات 35 الی 42، خرداد و تیر ماه 1401» به لینک زیر بروید.
vibration theory
In The Name Of God
Hello my friends, I,m Saeid Kordizade.
A senior mechanical engineer.
In this article, I intend to tell you about vibration theory.You may ask me this question that we could not see the spring and damper around the turbine.
In answering, suppose you want to change the rotor in a turbine shaft into a mathematics model.
So, you may place all body of eight meter rotor in weight of 2 ton in a component in the name of “m”.
the rotor springiness is called “k” and imposed damping to the rotor due to oil film and friction is substituted in “c” component.
the answer of your rotor
and finally, we get this equation:
The solution of this equation is the answer of your rotor.
unbalanced force
Now, suppose the unbalanced force is added to the rotor set.
In this position, we can not model the rotor vibration by the previous equation and the following equation must be written:
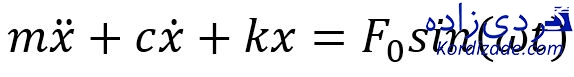
The answer is:
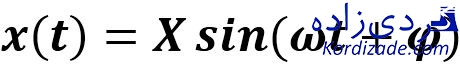
The amounts φ , X in terms of m, c, k, w is as follow:
An interesting note is the unbalanced force and answer have equal frequency and this is very useful for knowing the faults in the machine.
On other hand, the answer is back as the φ angle from excitation force(for example unbalanced force) .
φ and X diagrams
Some diagrams, make model the amounts φ and X in term of the observe in these diagrams, when the machine‘s rotor is closing to the natural frequency of machine, the amplitude is increased.
This problem shows the significance of oil film in the big machines, because big mashines can’t pass the natural frequency with critical speed by ball bearing and you must use a journal bearing.
Another note in the diagram is, when the machine is crossing from its natural frequency, its vibration amplitude is reduced.
It shows that big machines may work better (easier) after crossing from the first natural frequency.
The φ curve is shown in terms of the rotor speed as you see,
in the critical speed, all the curves pass from φ = 90.
This is useful for detecting the natural frequency.
As, the machine‘s natural frequency is where the phase angle is 90 ° and the vibration amplitude is maximum.
how many natural frequencies a system has?
You may ask that, how many natural frequencies a system has?
A system has infinite natural frequency and number of natural frequencies is depended to the way you have mathematically modeled the machine,
and the rate of necessity that you may aware from the third, forth and fifth frequencies in a machine.
Generally, we consider those natural frequencies in a system that their amounts are less than system frequency.
For example, as the distance between two supports are low in the small electromotors,
thus the k in electromotor is high. Also, the small electromotors have a low mass, thus, the natural frequency with “w” is big and more than the work rotor of electromotor.
Therefore, the natural frequency is not considered for small electromotors.
But, there will be computed to four natural frequencies for the turbines. Thanks your following.
